Kinematika

Dalam fisika, kinematika adalah cabang dari mekanika yang membahas gerakan benda tanpa mempersoalkan gaya penyebab gerakan. Hal terakhir ini berbeda dari dinamika atau sering disebut dengan Kinetika, yang mempersoalkan gaya yang memengaruhi gerakan.
Karena relatif sederhana, kinematika biasanya diajarkan sebelum dinamika atau sebelum konsep mengenai gaya diperkenalkan.

Daftar isi

Persamaan Dasar

Gerak Relatif

Dapat ditunjukkan dengan persamaan matematika vektor sederhana berikut yang memperlihatkan suatu penjumlahan vektor : gerak $A$ relatif terhadap $O$ sama dengan gerak relatif $B$ terhadap $O$ ditambah dengan gerak relatif $A$ terhadap $B$ :
$r_{A/O} = r_{B/O} + r_{A/B} \,\!$

Gerakan Koordinat

Salah satu persamaan dasar dalam kinematika adalah persamaan yang menggambarkan tentang turunan dari sebuah vektor yang berada dalam suatu sumbu koordinat bergerak. Yaitu : turunan terhadap waktu dari sebuah vektor relatif terhadap suatu koordinat diam, sama dengan turunan terhadap waktu vektor tersebut relatif terhadap koordinat bergerak ditambah dengan hasil perkalian silang dari kecepatan sudut koordinat bergerak dengan vektor itu. Dalam bentuk persamaan :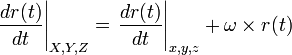
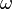$\left.\frac{dr(t)}{dt}\right|_{X,Y,Z} = \left.\frac{dr(t)}{dt}\right|_{x,y,z} + \omega \times r(t)$ dimana :
$r(t)$ adalah sebuah vektor
$X, Y, Z$ adalah sebuah sumbu koordinat tetap / tak bergerak
$x, y, z$ adalah sebuah sumbu koordinat berputar
$\omega$ adalah kecepatan sudut perputaran koordinat

Sistem Koordinat

Sistem Koordinat Diam

Pada sistem koordinat ini, sebuah vektor digambarkan sebagai suatu penjumlahan dari vektor-vektor yang searah dengan sumbu $X$ , $Y$ , atau $Z$ . Umumnya $\vec i \, \!$ adalah sebuah vektor satuan pada arah $X$ , $\vec j \, \!$ adalah sebuah vektor satuan pada arah $Y$ , dan $\vec k \, \!$ adalah sebuah vektor satuan pada arah $Z$ .
Vektor posisi $\vec s \, \!$ (atau $\vec r \, \!$ ), vektor kecepatan $\vec v \, \!$ dan vektor percepatan $\vec a \, \!$ , dalam sistem koordinat Cartesian digambarkan sebagai berikut :
$\vec s = x \vec i + y \vec j + z \vec k \, \!$
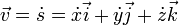
$\vec v = \dot {s} = \dot {x} \vec {i} + \dot {y} \vec {j} + \dot {z} \vec {k} \, \!$
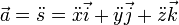
$\vec a = \ddot {s} = \ddot {x} \vec {i} + \ddot {y} \vec {j} + \ddot {z} \vec {k} \, \!$
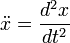
catatan : $\dot {x} = \frac{dx}{dt}$ , $\ddot {x} = \frac{d^2x}{dt^2}$

Sistem Koordinat Bergerak 2 Dimensi

Sistem koordinat ini hanya menggambarkan gerak bidang yang berbasis pada 3 vektor satuan orthogonal yaitu vektor satuan $\vec i \!$ , dan vektor satuan $\vec j \!$ sebagai sebuah bidang dimana suatu obyek benda berputar terletak/berada, dan $\vec k \!$ sebagai sumbu putarnya.
Berbeda dengan sistem koordinat Cartesian di atas, dimana segala sesuatunya diukur relatif terhadap datum yang tetap dan diam tak berputar, datum dari koordinat-koordinat ini dapat berputar dan berpindah - mengikuti gerakan dari benda atau partikel pada suatu benda yang diamati. Hubungan antara koordinat diam dan koordinat berputar dan bergerak ini dapat dilihat lebih rinci pada Transformasi Orthogonal.